A stochastic flight problem simulation to minimize cost of refuelling

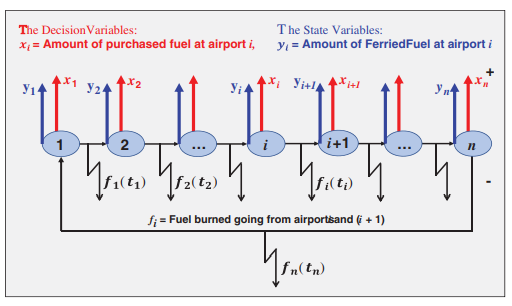
Commercial airline companies are continuously seeking to implement strategies for minimizing costs of fuel for their flight routes as acquiring jet fuel represents a significant part of operating and managing expenses for airline activities. A nonlinear mixed binary mathematical programming model for the airline fuel task is presented to minimize the total cost of refueling in an entire flight route problem. The model is enhanced to include possible discounts in fuel prices, which are performed by adding dummy variables and some restrictive constraints, or by fitting a suitable distribution function that relates prices to purchased quantities. The obtained fuel plan explains exactly the amounts of fuel in gallons to be purchased from each airport considering tankering strategy while minimizing the pertinent cost of the whole flight route. The relation between the amount of extra burnt fuel taken through tinkering strategy and the total flight time is also considered. A case study is introduced for a certain flight rotation in domestic US air transport route. The mathematical model including stepped discounted fuel prices is formulated. The problem has a stochastic nature as the total flight time is a random variable, the stochastic nature of the problem is realistic and more appropriate than the deterministic case. The stochastic style of the problem is simulated by introducing a suitable probability distribution for the flight time duration and generating enough number of runs to mimic the probabilistic real situation. Many similar real application problems are modelled as nonlinear mixed binary ones that are difficult to handle by exact methods. Therefore, metaheuristic approaches are widely used in treating such different optimization tasks. In this paper, a gaining sharing knowledge-based procedure is used to handle the mathematical model. The algorithm basically based on the process of gaining and sharing knowledge throughout the human lifetime. The generated simulation runs of the example are solved using the proposed algorithm, and the resulting distribution outputs for the optimum purchased fuel amounts from each airport and for the total cost and are obtained. © 2021 Tech Science Press. All rights reserved.