Fractional order oscillators based on operational transresistance amplifiers
In this paper, a general analysis of the fractional order operational transresistance amplifiers (OTRA) based oscillator is presented and validated through eight different circuits which represent two classifications according to the number of OTRAs. The general analytical formulas of the oscillation frequency, condition as well as the phase difference are illustrated for each case and summarized in tables. One of the advantages of the fractional-order circuit is the extra degrees of freedom added from the fractional-order parameters. Moreover different special cases {α = β ≢ 1, β ≢ α = 1, α ≢
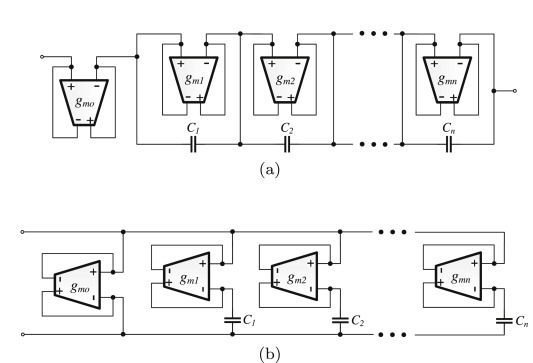
Realizations of simple fractional-order capacitor emulators with electronically-tunable capacitance
A novel resistorless topology for implementing fractional-order capacitor emulators, based on the employment of Operational Transconductance Amplifiers (OTAs) as active elements, is presented in this paper. The benefits of this topology are its simplicity in terms of component count, compared to other existing topologies in the literature, in addition to its electronic tunability. The performance of the presented topology is evaluated using Cadence and the 0.35 μm CMOS process Design Kit from Austria Mikro Systeme. Experimental results using commercial OTA chips are also provided, where the
Approximation of the fractional-order laplacian Sα as a weighted sum of first-order high-pass filters
A new approximation method of the fractional-order Laplacian operator sα is introduced. The approximation is based on a weighted sum of first-order filter sections and its analytical proof is given. The optimal high-pass filter section parameters that cover six frequency decades are obtained using the flower pollination algorithm while the effect of the number of filter sections on the accuracy of the approximation is investigated. Approximations of fractional-order capacitors of orders α =0.5 and α =0.7 synthesized in Foster-II form are given as a validating example. Further, an active
Fractional-order multi-phase oscillators design and analysis suitable for higher-order PSK applications
Recently, multi-phase oscillator design witnesses a lot of progress in communication especially phase shift keying based systems. Yet, there is a lack in design multi-phase oscillator with different fractional phase shifts. Thus, in this paper, a new technique to design and analyze a multi-phase oscillator is proposed. The proposed procedure is built based on the fractional-order elements or constant phase elements in order to generate equal or different phase shifts. The general characteristics equation for any oscillator is studied to derive expressions for the oscillation conditions and
Fractional order oscillators with single non-zero transmission matrix element
This paper presents a study of fractional order oscillator design based on a matrix. The presented oscillator consists of a general two port network and three impedances. Only two port with single element in its transmission matrix is discussed which gives four possible networks. Different combinations for one element have been investigated. The impedances associated with the studied networks are series or parallel connection of resistors in addition to fractional order capacitors. The characteristic equation, oscillation frequency and condition for each combination are introduced. Numerical
Fractional order two port network oscillator with equal order
Most of electric circuits can be viewed as a two port network with two terminals defined as input and output ports. In this paper, two different concepts are combined together which are the two port network concept and the fractional calculus to design a general fractional order two port network with equal order. An oscillator case study with three impedances structure has been presented. The three impedances are two equal order fractional capacitors and a resistor. Two different two port network are studied which are Op-amp based circuit and nonideal gyrator circuit. The general oscillation
Fractional-order RC and RL circuits
This paper is a step forward to generalize the fundamentals of the conventional RC and RL circuits in fractional-order sense. The effect of fractional orders is the key factor for extra freedom, more flexibility, and novelty. The conditions for RC and RL circuits to act as pure imaginary impedances are derived, which are unrealizable in the conventional case. In addition, the sensitivity analyses of the magnitude and phase response with respect to all parameters showing the locations of these critical values are discussed. A qualitative revision for the fractional RC and RL circuits in the
Fractional-Order Oscillators Based on Double Op-Amp
In this paper, complete analysis and design for fractional-order oscillators based on double Op-Amp are presented. The fractional order parameters enrich the oscillator design by offering the extra degree of freedom which adds more flexibility to the design. Two oscillators with double op-Amp are introduced. The oscillation frequency, condition, phase difference and the characteristic equation for each exhibited oscillator circuit are deduced in terms of the state matrix elements and the fractional order parameters. MATLAB simulations are discussed to validate the effect of the fractional
Fractional order integrator/differentiator: FPGA implementation and FOPID controller application
This paper introduces two FPGA based design approaches of the fractional order integrator and differentiator using Grünwald Letnikov (GL) definition where fixed window and linear approximation approaches are considered. The main advantage of the linear approximation method is that it reduces the huge memory of the fractional order systems. One of the top applications of fractional calculus is the fractional order Proportional Integral Derivative (FOPID) controller. It has gained a great attention in academic studies and in industrial applications. The proposed approaches have been used as
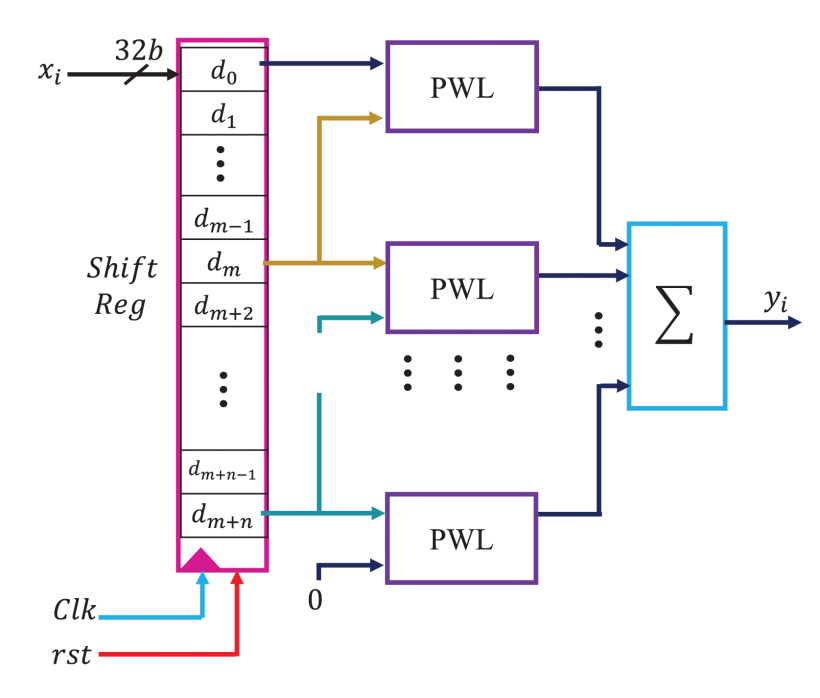
FPGA Implementation of the Fractional Order Integrator/Differentiator: Two Approaches and Applications
Exploring the use of fractional calculus is essential for it to be used properly in various applications. Implementing the fractional operator Dα in FPGA is an important research topic in fractional calculus; in the literature, only a few FPGA implementations have been proposed due to the memory dependence of the fractional order systems. In this paper, FPGA implementations of fractional order integrator/differentiator based on the Grünwald-Letnikov (GL) operator are proposed. Two algorithms are developed based on look-up table and quadratic and piece-wise linear approximation approaches to
Pagination
- Previous page ‹‹
- Page 29
- Next page ››
