Elmore delay in the fractional order domain
Interconnect design has recently become one of the important factors that affect the circuit delay and performance especially in the deep submicron technology. The modelling of interconnects is typically based on using Elmore definitions of the delay time and rise time. So, a general formula for Elmore delay time and rise time in the fractional order domain are presented in this work. It is found from the new formulas of the delay time and rise time that these timing values could be controlled or tuned by the fractional orders. Hence, the fractional order can compensate for the components
Electronically tunable fractional-order highpass filter for phantom electroencephalographic system model implementation
The fractional-order model of a phantom electroencephalographic system, at various distances between electrodes, is realized using appropriate decomposition of the rational transfer functions which approximate the highpass filters that describe its dynamics. The main offered benefits, in comparison to the corresponding straightforward implementations of the rational transfer functions, are the capability of monolithic implementation due the minimization of the maximum value of the required capacitances and, also, the reduced power consumption. The performance of the presented filter topologies
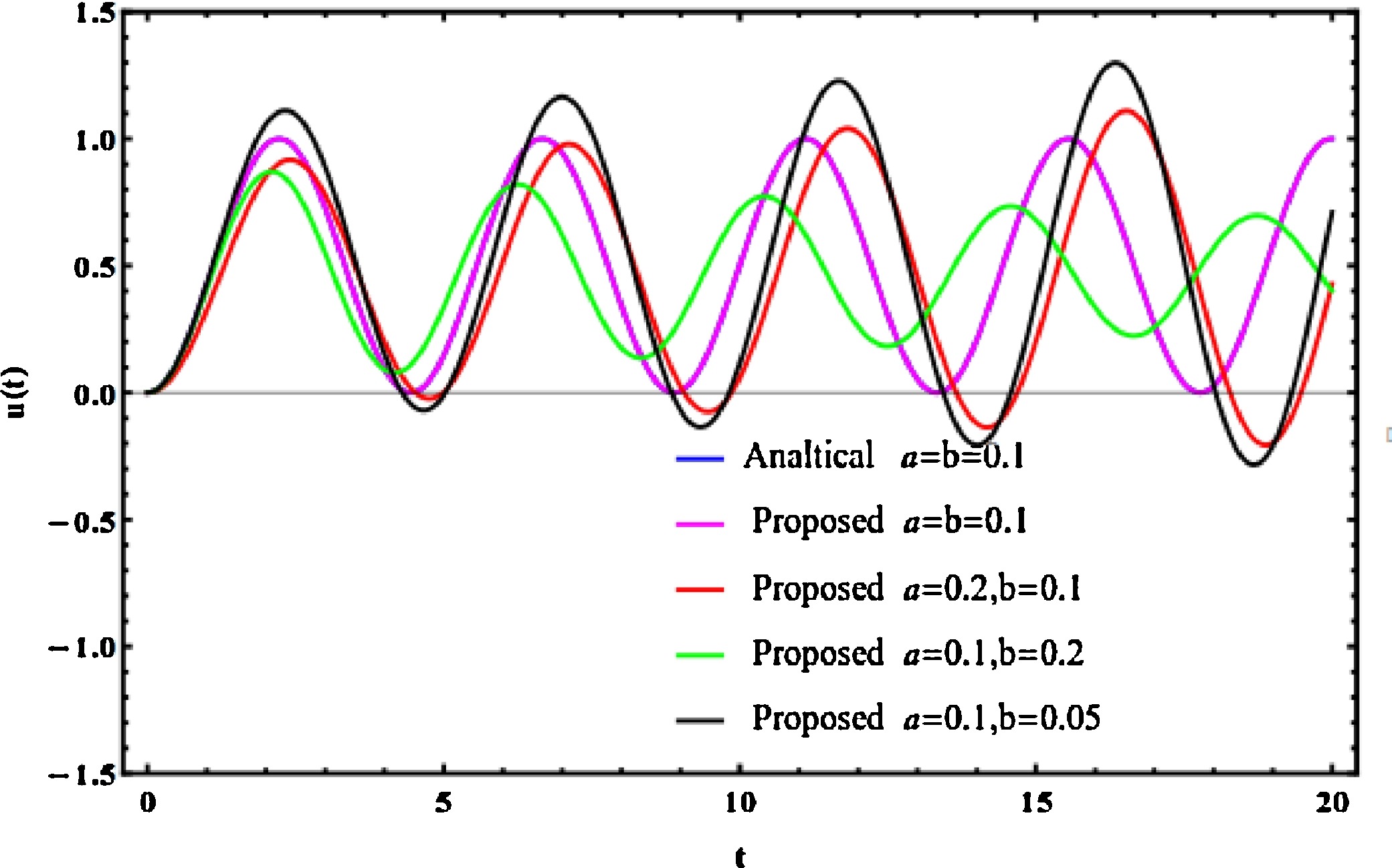
Modified methods for solving two classes of distributed order linear fractional differential equations
This paper introduces two methods for the numerical solution of distributed order linear fractional differential equations. The first method focuses on initial value problems (IVPs) and based on the αth Caputo fractional definition with the shifted Chebyshev operational matrix of fractional integration. By applying this method, the IVPs are converted into simple linear differential equations which can be easily handled. The other method focuses on boundary value problems (BVPs) based on Picard's method frame. This method is based on iterative formula contains an auxiliary parameter which
Electrochemical stability analysis of red phosphorus-based anode for lithium-ion batteries
Red phosphorus and sulfurized polyacrylonitrile (RP-SPAN) composite has recently shown promising results as an anode material in lithium-ion battery applications. However, the stability analysis of its dynamic response has not been investigated yet. In this study we use the transfer function stability analysis, the Kramers-Kronig (KK) integral relations, and the differential capacity analysis to evaluate the cell's behavior in both frequency and time domains in terms of stationarity, stability, linearity, as well as dissipation and degradation with extended charge/discharge cycling. The
On new fractional inverse matrix projective synchronization schemes
In this study, the problem of inverse matrix projective synchronization (IMPS) between different dimensional fractional order chaotic systems is investigated. Based on fractional order Lyapunov approach and stability theory of fractional order linear systems, new complex schemes are proposed to achieve inverse matrix projective synchronization (IMPS) between n-dimension and m-dimension fractional order chaotic systems. To validate the theoretical results and to verify the effectiveness of the proposed schemes, numerical applications and computer simulations are used. © Springer International
On new fractional inverse matrix projective synchronization schemes
In this study, the problem of inverse matrix projective synchronization (IMPS) between different dimensional fractional order chaotic systems is investigated. Based on fractional order Lyapunov approach and stability theory of fractional order linear systems, new complex schemes are proposed to achieve inverse matrix projective synchronization (IMPS) between n-dimension and m-dimension fractional order chaotic systems. To validate the theoretical results and to verify the effectiveness of the proposed schemes, numerical applications and computer simulations are used. © Springer International
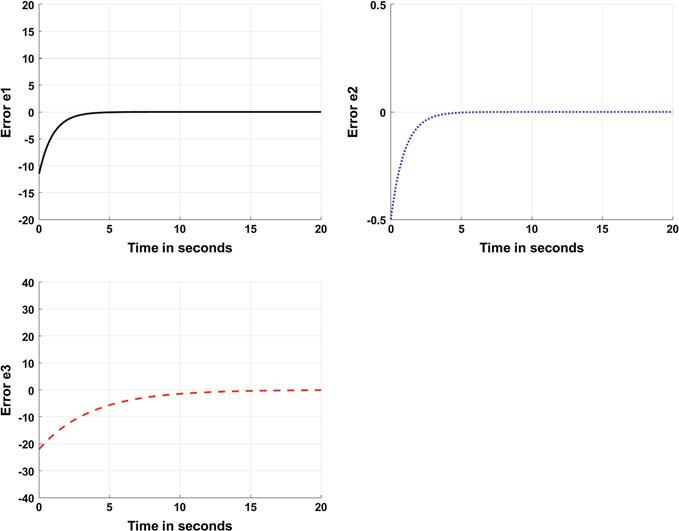
A new method to synchronize fractional chaotic systems with different dimensions
By using two scaling function matrices, the synchronization problem of different dimensional fractional order chaotic systems in different dimensions is developed in this chapter. The controller is designed to assure that the synchronization of two different dimensional fractional order chaotic systems is achieved using the Lyapunov direct method.Numerical examples and computer simulations are used to validate numerically the proposed synchronization schemes. © Springer International Publishing AG 2017. All rights reserved.

A new method to synchronize fractional chaotic systems with different dimensions
By using two scaling function matrices, the synchronization problem of different dimensional fractional order chaotic systems in different dimensions is developed in this chapter. The controller is designed to assure that the synchronization of two different dimensional fractional order chaotic systems is achieved using the Lyapunov direct method.Numerical examples and computer simulations are used to validate numerically the proposed synchronization schemes. © Springer International Publishing AG 2017.
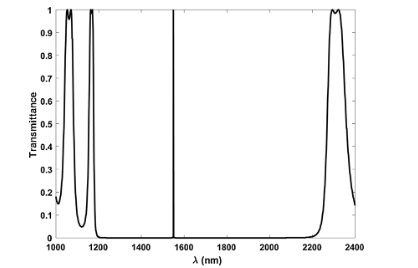
Stochastic analysis for one dimensional photonic crystals
Tolerance variations of the design parameters of the photonic crystals due to fabrication processes have a strong effect on the performance of the photonic crystals and their operating wavelengths. In this work, the uncertainties of the design parameters of one-dimensional photonic crystals (1D-PCs) and their impacts on the PCs optical properties and the operating performance are investigated. The effects of these uncertainties for different tolerances are studied for both defect-free PCs and PCs with a defect air layer. The probability distribution function and the standard deviations of the
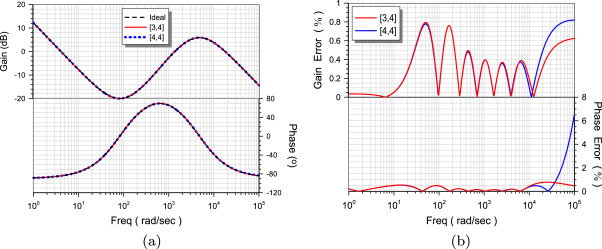
Realizations of fractional-order PID loop-shaping controller for mechatronic applications
A novel procedure for the realization of a fractional-order PID loop-shaping controller, suitable for precision control of mechatronic systems, is introduced in this work. Exploiting appropriate tools, the controller function is approximated as a whole, leading to a simple form of integer-order approximation, when compared to the case where each intermediate part of the PID transfer function is approximated. This leads to a direct implementation, composed of conventional active and passive elements. Simulation and experimental results, derived from the OrCAD PSpice simulator and a Field
Pagination
- Previous page ‹‹
- Page 39
- Next page ››
